Đề thi thử THPT Quốc gia môn Toán năm 2019 - Đề 1 - Sở GD&ĐT Kon Tum (Có đáp án chi tiết)

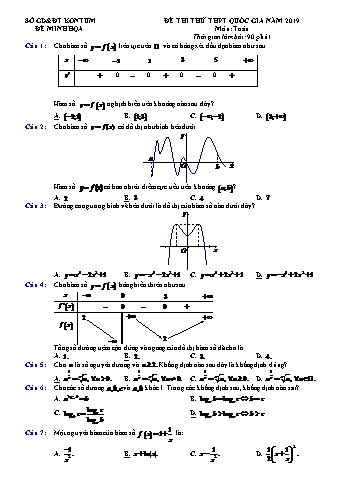
 ít nhất ba cạnh.	B. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
C. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.	D. Mỗi mặt có ít nhất ba cạnh.
Cho khối cầu có thể tích bằng Tính bán kính mặt cầu.
A. 	B. 	C. 	D. 
Trong không gian với hệ tọa độ , cho ba điểm . Tính tích vô hướng 
A. 	B. 	C. 	D. 
Trong không gian với hệ tọa độ , xác định tọa độ tâm và bán kính của mặt cầu có phương trình .
A. .	B. .
C. .	D. .
Trong không gian với hệ tọa độ cho mặt phẳng Mặt phẳng có vectơ pháp tuyến là
A. 	B. 	C. 	D. 
Cho dãy số: . Tìm các giá trị dương của để dãy số đã cho theo thứ tự lập thành cấp số nhân?
A. 4.	B. 	C. .	D. .
Đồ thị hàm số có tiệm cận đứng là đường thẳng nào sau đây?
A. .	B. .	C. .	D. .
Cho hàm số xác định, liên tục trên và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị.	B. Hàm số có giá trị cực tiểu bằng .
C. Hàm số có giá trị lớn nhất bằng 	D. Hàm số đạt cực đại tại 
Nếu thì
A. .	B. .	C. .	D. .
Cho . Khi đó giá trị của được tính theo là :
A. .	B. .	C. .	D. .
Tập nghiệm của bất phương trình là
A. .	B. .	C. .	D. .
Cho hàm số Đạo hàm bằng
A. 	B. 	C. 	D. 
Biết là một nguyên hàm của của hàm số và đồ thị hàm số đi qua điểm . Tính 
A. .	B. .
C. .	D. .
Trong tập số phức cho và là hai nghiệm của phương trình Tìm số phức liên hợp của số phức 
A. 	B. 	C. 	D. 
Trong mặt phẳng Oxy, gọi lần lượt là các điểm biểu diễn các số phức Gọi là trọng tâm của tam giác Hỏi là điểm biểu diễn số phức nào trong các số phức sau?
A. 	B. 	C. 	D. 
Cho hình chóp có đáy là tam giác vuông tại , , , , . Thể tích của khối chóp bằng
A. .	B. .	C. .	D. .
Một hình lập phương cạnh bằng nội tiếp khối cầu và ngoại tiếp khối cầu Gọi và lần lượt là thể tích của các khối và . Tính tỉ số .
A. .	B. .	C. .	D. .
Cho mặt cầu có bán kính là a, ngoại tiếp hình nón. Thiết diện qua trục của hình nón là tam giác đều. Tính thể tích của khối nón đó.
A. 	B. 	C. 	D. 
Trong không gian với hệ tọa độ cho mặt cầu có phương trình và mặt phẳng...o hai đường thẳng và . Một mặt phẳng vuông góc với cắt trục tại và cắt tại . Tìm độ dài nhỏ nhất của đoạn 
A. .	B. .	C. .	D. .
Cho hình chóp có đáy là hình thang vuông tại , đáy lớn , . vuông góc với mặt phẳng , . Gọi là trung điểm của cạnh . Gọi là mặt phẳng qua và vuông góc với . Thiết diện tạo bởi và hình chóp có diện tích bằng
A. .	B. .	C. .	D. .
Cho dãy số với . Số hạng tổng quát của dãy số là số hạng nào dưới đây?
A. .	B. .	C. .	D. .
Một người gửi tiết kiệm với lãi suất một năm và lãi hàng năm được nhập vào vốn. Sau ít nhất bao nhiêu năm người đó nhận được số tiền lớn hơn số tiền gửi ban đầu? ( Biết lãi suất không thay đổi qua các năm ông gửi tiền).
A. năm.	B. năm.	C. năm.	D. năm.
Cho , , là các số thực dương thỏa mãn , , . Tính giá trị .
A. .	B. .	C. .	D. .
Cho hàm số Đồ thị hàm số như hình bên dưới
Hàm số nghịch biến trên khoảng nào trong các khoảng sau?
A. 	B. 	C. 	D. 
Cho hàm số có bảng biến thiên như hình vẽ bên dưới
Đồ thị hàm số có điểm cực trị khi
A. 	B. 	C. 	D. 
Có bao nhiêu giá trị nguyên của thuộc khoảng để hàm số đồng biến trên 
A. 	B. 	C. 	D. 
Với hai số phức và thỏa mãn và Tìm giá trị lớn nhất của 
A. 	B. 	C. 	D. 
Cho hình chópNguyễn Thành Luận
 có đáy là tam giác vuông cân tại , , , , . Gọi , lần lượt là trung điểm , . Gọi là góc giữa với . Tính .
A. .	B. .	C. .	D. .
Viết phương trình mặt cầu có tâm và cắt trục Oz tại hai điểm A, B sao cho diện tích tam giác IAB bằng 
A. 	B. 
C. 	D. 
Cho đa giác đều có đỉnh. Chọn ngẫu nhiên đỉnh của đa giác đều, xác suất để đỉnh được chọn là đỉnh của một tam giác vuông không cân là
A. 	B. 	C. 	D. 
Một vật đang chuyển động với vận tốc (m/s) thì thay đổi vận tốc với gia tốc được tính theo thời gian t là . Tính quãng đường vật đi được kể từ thời điểm thay đổi gia tốc đến lúc vật đạt vận tốc nhỏ nhất.
A. (m)	B. 104 (m).	C. 208 (m).	D. (m).
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có điểm M là trung điểm của đoạn AB và N là điểm thuộc đoạn AC sao cho Tính độ dài cạnh của hì...ghịch biến trên các khoảng và 
Đồ thị hàm số cát trục hoành tại 3 điểm phân biệt. Do đó:
Ta có: 
Để hàm số đồng biến trên thì với mọi .
Suy ra với mọi , 
Xét hàm số ta có , 
. Để với mọi thì 
Hướng dẫn giải
 Đặt ( với là gốc tọa độ, là điểm biểu diễn của ).
 Dựng hình bình hành khi đó ta có 
Theo định lý đường trung tuyến ta có 
Ta có 
Hướng dẫn giải
Gọi là hình chiếu của lên , ta có: và .
Mà là tam giác vuông cân tại nên là hình vuông.
Gọi là trung điểm của , ta có mà .
Do đó là hình chiếu của lên ..
; .
; .
Câu 46: Hướng dẫn giải:
Gọi H là hình chiếu của trên Oz
Vậy phương trình mặt cầu là: 
Hướng dẫn giải. 
● Số tam giác vuông là 
● Số tam giác vuông cân: Cứ mỗi cách chọn đường kính là có tam giác cân ( điểm tạo nên tam giác cân là giao điểm của đường thẳng qua tâm vuông góc với đường kính đã chọn với đường tròn). Do đó có tam giác vuông cân.
Suy ra : 
Hướng dẫn giải: Ta có mà 
Khi đó Suy ra 
Vậy quãng đường vật đi được trong 2s là 
Hướng dẫn giải: Gọi a là cạnh của hình vuông.
Ta có: 
Hướng dẫn giải: Đặt , ta thu được Suy ra 
Từ , ta đổi cận Khi đó